- Published on
Analyzing the Impact of Lagged Features in Time Series Forecasting: A Linear Regression Approach
- Authors
- Name
- Name
Abstract
Context: Time series analysis involves understanding patterns in data collected over time to predict future trends. Lagged features, representing past values of a variable, are crucial in this analysis to incorporate the temporal dependencies within the dataset.
Problem: Predictive modeling in time series often needs help accurately forecasting future values, especially in the presence of noise and complex underlying patterns. The challenge is to use historical data to predict future outcomes effectively.
Approach: A synthetic time series dataset was generated to simulate a scenario with linear trends and added noise. Lagged features were created by shifting the time series, and a simple linear regression model was employed to predict future values based on these features.
Results: The linear regression model yielded a mean squared error (MSE) of 185.38 and an R² score of -3.02, indicating a poor fit and predictive performance worse than a naive mean-based model.
Conclusions: The negative R² score and high MSE highlight the limitations of using a simple linear regression model with only one lagged feature for time series prediction, especially in datasets with noise and non-linear trends. This underscores the necessity for more sophisticated modeling techniques or additional explanatory variables to improve forecasting accuracy in time series analysis.
Keywords: Time Series Analysis; Lagged Features; Predictive Modeling; Linear Regression; Forecasting Accuracy.
Introduction
Time series analysis is a critical component of statistical studies and machine learning that involves analyzing data points collected over time to extract meaningful statistics and characteristics. Lagged features, a fundamental concept in time series analysis, are pivotal in developing predictive models that forecast future events based on historical data. This essay explores the idea of lagged features, their importance in time series forecasting, how they are created, and their application in various predictive modeling techniques.
Time reveals patterns, and patterns predict the future. In the dance of data, lagged features lead the steps to foresight.
Understanding Lagged Features
Lagged features refer to data from previous periods used as input to model future periods in a time series. They are essentially the past values of a dataset, shifted backward in time, serving as a mirror to the historical patterns and trends likely to influence future outcomes. By analyzing how past events affect future occurrences, lagged features help understand the data's temporal dependencies.
For instance, in financial markets, the price of a stock on a given day can be influenced by its prices on preceding days. Here, the lagged features would be the stock prices from the previous days, and these historical values are used to predict the stock's future price.
Background
Lagged features in data analysis refer to past values of a variable used to predict future values of the same variable. They are a common technique in time series forecasting, where previous data points are used to forecast future ones. Here’s a breakdown of the concept:
- Time Series Data: This is a sequence of data points collected or recorded regularly. Examples include daily stock prices, monthly sales data, and yearly temperature readings.
- Lagging: This involves shifting the time series data backward by specific periods. For example, if you have daily sales data, a one-day lagged feature would be the sales data from the previous day.
- Forecasting and Analysis: Lagged features are used in predictive modeling to help the model understand patterns over time. For instance, to forecast tomorrow’s sales, you might use sales data from the past week as lagged features.
- Creating Lagged Features: This is done by taking the original time series and creating new columns (features) for each lagged time step you want to consider. For example, if you are working with a time series of daily temperatures, you might create a lagged feature for the temperature one day ago, another for two days ago, and so on.
- Importance in Models: Lagged features are crucial in time series models like ARIMA (Autoregressive Integrated Moving Average), LSTM (Long Short-Term Memory Networks), and other machine learning algorithms that predict future trends based on past data.
By incorporating lagged features, models can capture temporal dependencies and patterns in the data, leading to more accurate predictions.
The Importance of Lagged Features
The significance of lagged features in time series analysis cannot be overstated. They provide a mechanism to capture the temporal dynamics of a dataset, allowing analysts and modelers to identify patterns, trends, and seasonality in historical data. This understanding is crucial for accurately forecasting future values, as it helps construct a model that accounts for past behavior to predict future occurrences.
In domains such as economics, meteorology, and healthcare, where past conditions often influence future events, lagged features are indispensable for making informed predictions. For example, understanding the lag effect of economic policies on market performance or the impact of historical weather patterns on future climate conditions relies heavily on analyzing lagged features.
Creating Lagged Features
Creating lagged features involves shifting the time series data so that each point in the series is aligned with its previous values at specified time intervals. This process transforms the dataset into a format where the model can easily recognize and learn from the historical patterns in the data.
In practice, this is achieved by introducing a lag period — one day, one month, or one year — and then shifting the data points accordingly to create new columns in the dataset, each representing a lagged version of the original series. The choice of lag period depends on the specific domain and the nature of the time series being analyzed. Careful consideration is required to ensure that the lagged features are meaningful and relevant to the predictive model.
Application in Predictive Modeling
Lagged features are integral to various predictive modeling techniques in time series analysis, including autoregressive models, machine learning algorithms, and deep learning approaches. In autoregressive models, for example, the future value of a variable is predicted based on a combination of its past values, with these past values serving as lagged features.
In machine learning, algorithms like Random Forests, Support Vector Machines (SVMs), and Neural Networks can incorporate lagged features to enhance their predictive capabilities. These features provide the historical context these models need to make accurate forecasts.
Furthermore, in advanced deep learning techniques, such as Long Short-Term Memory (LSTM) networks, lagged features are crucial for capturing long-term dependencies in time series data, allowing these models to make predictions based on long-range historical patterns.
Mathematical Foundations
We can consider a simple linear regression model to delve into the mathematical aspect of lagged features and their use in predictive modeling. Here are the fundamental equations:
Lagged Feature Definition:
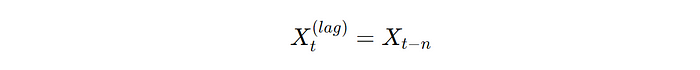
where Xt(lag) is the lagged feature at time t, _Xt_ is the original feature at time t, and n is the lag period.
Linear Regression Model: The model predicting the current value based on lagged features is represented as:
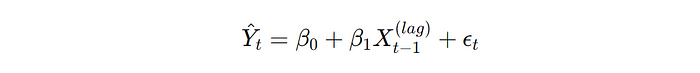
where Y^_t_ is the predicted value at time _β_0 is the intercept, _β_1 is the coefficient for the lagged feature, _Xt_−1(lag) is the lagged feature at time _t_−1, and _ϵt_ is the error term.
Mean Squared Error (MSE): The MSE is used to measure the average of the squares of the errors, that is, the average squared difference between the estimated values and the actual value:
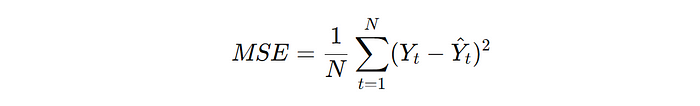
where N is the number of observations, _Yt_ is the actual value at time t, and Y^_t_ is the predicted value at time t.
Coefficient of Determination (_R_2): The _R_2 statistic provides a measure of how well the observed outcomes are replicated by the model, based on the proportion of total variation of outcomes explained by the model:
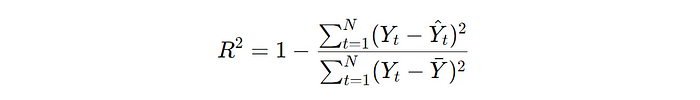
where ˉ_Y_ˉ is the mean of the actual values _Yt_.
These equations form the mathematical foundation for analyzing time series data with lagged features, allowing for the quantification of relationships between past and future values in a dataset.
Code
To demonstrate the concept of lagged features, let's create a synthetic dataset, use it to train a simple predictive model, and then evaluate the model's performance. We'll also generate plots to visualize the results and interpret them. Here's how we can do this in Python:
- Generate a Synthetic Dataset: Create a time series dataset.
- Create Lagged Features: Transform the dataset to include lagged features.
- Build and Train a Model: Use a simple linear regression model for prediction.
- Evaluate the Model: Calculate metrics and visualize the results.
Let's start by writing the complete Python code to implement these steps:
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# 1. Generate a Synthetic Dataset
np.random.seed(42)
time = np.arange(100)
value = time * 0.5 + np.random.normal(size=100) * 10 # Linear trend with noise
# Convert to a pandas DataFrame
data = pd.DataFrame({'Time': time, 'Value': value})
# 2. Create Lagged Features
lag_periods = 1
data['Lagged_Value'] = data['Value'].shift(lag_periods)
data.dropna(inplace=True) # Remove rows with NaN values due to shifting
# 3. Build and Train a Model
X = data[['Lagged_Value']] # Features
y = data['Value'] # Target variable
# Split the dataset into train and test sets
split_ratio = 0.8
split_index = int(len(data) * split_ratio)
X_train, X_test = X[:split_index], X[split_index:]
y_train, y_test = y[:split_index], y[split_index:]
# Train the linear regression model
model = LinearRegression()
model.fit(X_train, y_train)
# Make predictions
predictions = model.predict(X_test)
# 4. Evaluate the Model
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
# Results and Interpretations
print(f'Mean Squared Error: {mse:.2f}')
print(f'R^2 Score: {r2:.2f}')
# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(data['Time'], data['Value'], label='Actual')
plt.plot(data['Time'][split_index:], predictions, label='Predicted')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Actual vs. Predicted Values')
plt.legend()
plt.show()
Interpretation:
- Mean Squared Error (MSE): This metric will provide us with the average squared difference between the actual and predicted values. Lower values indicate a better fit.
- R² Score: Represents the proportion of the variance in the dependent variable that is predictable from the independent variables. An R² score close to 1 indicates a model that explains much of the variance.
In the plot, we should see the actual time series and the predictions made by the model. The linear relationship between the lagged values and the current values will be evident, and the performance metrics will give us a quantitative measure of how well the model predicts the time series data based on its lagged features.
The results from executing the code are as follows:
- Mean Squared Error (MSE): 185.38
- R² Score: -3.02
Interpretation
- Mean Squared Error (MSE): The MSE of 185.38 indicates the average squared differences between the actual and predicted values. In this context, the value suggests that the model's predictions are, on average, about 185.38 units squared away from the actual values.
- R² Score: The R² score of -3.02 is quite unusual because R² typically ranges between 0 and 1 for most models. A negative R² indicates that the model performs worse than a simple horizontal line representing the mean of the dependent variable. This result suggests that the model does not fit the data well and is not a good predictor for this dataset.
The negative R² score might be due to the simplicity of the model (linear regression with only one lagged feature), the random noise in the synthetic data, or the model's inability to capture the underlying pattern of the dataset. This highlights the importance of model selection and testing different hypotheses in time series forecasting.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# 1. Generate a Synthetic Dataset
np.random.seed(42)
time = np.arange(100)
value = time * 0.5 + np.random.normal(size=100) * 10 # Linear trend with noise
# Convert to a pandas DataFrame
data = pd.DataFrame({'Time': time, 'Value': value})
# 2. Create Lagged Features
lag_periods = 1
data['Lagged_Value'] = data['Value'].shift(lag_periods)
data.dropna(inplace=True) # Remove rows with NaN values due to shifting
# 3. Build and Train a Model
X = data[['Lagged_Value']] # Features
y = data['Value'] # Target variable
# Split the dataset into train and test sets
split_ratio = 0.8
split_index = int(len(data) * split_ratio)
X_train, X_test = X[:split_index], X[split_index:]
y_train, y_test = y[:split_index], y[split_index:]
# Train the linear regression model
model = LinearRegression()
model.fit(X_train, y_train)
# Make predictions
predictions = model.predict(X_test)
# 4. Evaluate the Model
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
# Results and Interpretations
mse, r2
Now let's visualize the actual vs. predicted values to get a clearer picture of the model performance:
The plot shows the actual values of the synthetic time series compared to the predicted values from the linear regression model. Here's what we can observe:
- The actual data shows a linear trend with some noise.
- The predicted values, indicated by the dashed line, deviate significantly from the actual values, especially towards the end of the series.
The discrepancy between the actual and predicted values explains the negative R² score. This model, a simple linear regression with one lagged feature, may not be sophisticated enough to accurately predict the time series, especially given the noise present in the data. This situation underscores the need for more complex modeling approaches or additional features to improve predictive accuracy in time series analysis.
Conclusion
Lagged features are a cornerstone of time series analysis, offering a window into the past to forecast the future. They enable the identification of patterns and dependencies in historical data, facilitating the development of robust predictive models. Whether in economic forecasting, weather prediction, or stock market analysis, lagged features help analysts and modelers make sense of the temporal dynamics in their data, leading to more accurate and reliable predictions. As such, understanding and effectively utilizing lagged features is essential for anyone involved in analyzing and forecasting time series data.
Time series causal relationships discovery through feature importance and ensemble models
Time-series forecasting through recurrent topology - Communications Engineering